4支队伍怎样安排比赛决出冠军最为合理?
4支队伍怎样安排比赛决出冠军最为合理大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!?合理,即用最少的场次,避免最小可能的意外,决出最公正的结果?数学专业的专家请进!
很不幸题目分类错了。
这个问题有一半属于社会选择理论(Social Choice Theory)。
先来讨论一个最平凡的情况:如果:A 胜过了 B、C、D;B 胜过了 C、D;D 负于 C;并且比赛结果实际上就反应了两个人之间的实力水平;那么毫无疑问,A 是第一,B 是第二, C 是第三,D 是第四。
问题在于现实生活中有随机因素和环。
所谓的随机因素就是,A 和 B 打十次,可能 6 胜 2 平 2 负。但是如果恰好撞到了 2 平或者 2 负的那一次,并且我们以这个为结果,那么 A 就有可能获得于自己实际水平不匹配的成绩。当然,这在体育比赛中是可以忽略的事情,毕竟赛事年年有,总不至于 A 实力强于 B 但是次次都负于 B,既然有赢有输,那就不必计较了。
如果我们一定要钻牛角尖,决出理想的结果,自然是让两两之间对决 100 次,然后根据总体上的胜负情况来看最后两个队伍之间的真正的实力对比是怎么样的,说不定还能将简单的胜负关系通过胜负场次的状况数值化为一种实力差之类的东西。并且,原则上来说,虽然在偶然的情况下可能有环,但是在大量比赛之后依然有环出现的概率会小很多。
麻烦的东西是环。
假定有 A>B>C>D>A (X>Y 表示在直接对决的时候 X 胜了 Y,毕竟单场比赛有运气因素,这也不是不可能的事情)。
如果采取世界杯决赛的方式,即,将四队分成两组,然后两组的胜者之间决出冠亚军,败者之间决出三四名,就会出现这样的情况:如果 A、B 在一组,那么 A 至少能获得亚军,而如果 D、A 在一组,那么 A 至多只能获得季军。
这也就是题主口中说的不合理的来源之一:环的存在。
即便我们进行了循环赛,我们也不一定能破解环,我先列一个最坑爹的情况:A>B,A>D;B>C,B>D;C>A,C>D;
毫无疑问,D 没戏了,但是 A、B、C 要怎么办?并列冠军?嘛,这样也好。但是直观上来说,我们只能接受 A、B、C 相互打平的时候以打平结束,而对于这种成环的情况,还是会忍不住用别的标准再来一决胜负。
这样说起来,虽然比赛和投票很像,但是还是有区别的。先说它们类似的地方吧:有若干个候选人(参赛者);目的是得到一个候选人(参赛者)的排序;公正的比赛和投票需要满足中立性:即结果由选票决定,而不由候选人位置决定(比如说,如果一个比赛总是让第一个登场的选手获得第一名,第二个第二名,那么它就不满足中立性)。
不同的地方在于:选票和比赛结果:一张选票是对于所有候选人的一个排序;一个比赛结果是对于两个候选人之间的一个排序。
(选票中的「>」具有传递性) 公正的投票需要满足匿名性:任何两张选票都是等效的,不会因为投票者是某个人而因此获得更大的权重,独裁是非匿名性的极致:独裁者的权重为 1,其他人没有权重。公正的比赛制度需要避免这种情况:(假定每场比赛都是胜者得 3 分,平各 1 分,负者 0 分)A 和 B 之间进行 10 场比赛,B 和 C 之间进行 3 场,A 和 C 之间进行 1 场比赛。(这两条是说:选票可以单方面叠加;但是比赛结果是不应该单方面叠加的,如果采取积分制度,只应该进行多轮比赛,不应该允许两方单独进行比赛,除非是为打破平局。选票可以叠加的根本原因在于:选票总是同时给出一个完整的排序,但是比赛永远只是在两个对手之间进行。)化约关系:一张选票总可以化约为 场比赛结果(n 是候选人数目,比如说 A>B>C 可以化约为三场比赛结果:A>B,A>C,B>C);但是两两之间的
场比赛结果(n 是候选人数目,比如说 A>B>C 可以化约为三场比赛结果:A>B,A>C,B>C);但是两两之间的 场比赛结果不一定能化约为一张选票(同样是三人的情况,A>B,B>C,C>A 以及 B>A,C>B,A>C 各自都不能化约为一张选票,但是将两者重新组合之后倒是有可能化约为如下两张选票:A>B>C 和 C>B>A,但是与此同时,我们也可以将这六个结果组合成如下两张选票:C>A>B 和 B>A>C ,这就充分体现了两者之间的差别)。
场比赛结果不一定能化约为一张选票(同样是三人的情况,A>B,B>C,C>A 以及 B>A,C>B,A>C 各自都不能化约为一张选票,但是将两者重新组合之后倒是有可能化约为如下两张选票:A>B>C 和 C>B>A,但是与此同时,我们也可以将这六个结果组合成如下两张选票:C>A>B 和 B>A>C ,这就充分体现了两者之间的差别)。
下面介绍一个比较新的概念:Condorcet 赢家。
将一张选票拆分为 个有序对,如果 A>B 的数目比 B>A 的数目多,那么 A 就胜于 B,如果 A 在和其它玩家的比较中都胜出了,那么 A 就是 Condorcet 赢家。正是由于这种计分法会把一张选票全部拆成两两对比的情况,因此它也适用与一般的比赛的结果判定中。
个有序对,如果 A>B 的数目比 B>A 的数目多,那么 A 就胜于 B,如果 A 在和其它玩家的比较中都胜出了,那么 A 就是 Condorcet 赢家。正是由于这种计分法会把一张选票全部拆成两两对比的情况,因此它也适用与一般的比赛的结果判定中。
当然,如果出现了环的话,Condorcet 赢家就不一定存在了。(关注赢家的另一个理由是,或许我们可以分别依次递归地决出 1、2、3、4 名,但是由于阿罗不可能性定理,我们知道这在某些情况下一定会带来违反独立无关性条件的结果。)
但是,虽然这个标准可以搬到比赛中来,这并不意味着这个标准就是一个没有争议的标准。毕竟在投票的时候,有可能 Condorcet 赢家是没有办法被其它投票方式选出的。考虑如下情况:3 张选票:A>B>C2 张选票:B>C>A1 张选票:B>A>C1 张选票:C>A>B
这时,A 是 Condorcet 赢家,因为 A 和 B 比较的时候 A 赢了 4 次输了 3 次;A 和 C 比较的时候也是如此。但是,如果我们采用另外一种方法,比如说让一张选票上的第一名得 x 分,第二名得 y 分,第三名得 z 分,只要满足 x>y>z,B 就一定会是赢家。(如果按照赢了比赛得 1 分,输了得 0 分的话,A=8,B=9,C=4,赢家竟然也不是 B,话说这特么和 Borda 计分法
(第一名得 n-1 分,依次递减,最后一名 0 分) 的结果是一样的,貌似我可以证明这个,嘛算了不证明了,你自己看的懂的)
位置计分法看上去只能适用于选票要求给出所有候选人的排序的情况,不一定适用于比赛这种两两对比的结果,况且就算能够转化,同一种比赛结果也会得到多种可能的选票组合,不过话说回来,(A>B>C + C>B>A)在 Borda 计分法下面是 A B C 各自得 2 分,而这和(C>A>B + B>A>C )的结果是一样的。看来我需要去考虑看看选票的组合方式在什么情况会受到影响,不过这是另一个问题了。或许我们可以证明,无论如何将比赛结果转化为选票,Borda 计分法的结果和认为赢了得 1 分输了不得分计算出来的积分数是一样的。
好的回归正题,由于 Condorcet 赢家的概念非常严苛,在大多数情况下都可能选不出恰当的赢家,所以最直接的办法就是将这种制度进行扩展,比如说:当没有 Condorcet 赢家的时候,我们将过去的比赛结果进行删除,每个选手的得分 x 是他至少需要删除 x 场才能成为 Condorcet 赢家。
比如说:A>B 4:1(表示 A>B 3 场, A<B 2 场)B>C 4:1C>A 3:2
在这种情况下,A、B、C 都不是 Condorcet 赢家,但是如果我们删除两场 C>A 的结果,那么就会出现 C<A 1:2 的情况,此时 A 就成为了 Condorcet 赢家。同理只要我们删除 4 场 A>B,B 就会变成 Condorcet 赢家,C 也要至少 4 场。因此最后的赢家是得分最少的 A。
说一下结论:Borda 积分制的本质就是:如果 A 赢了 B 一场,那么 A 得 1 分,B 不得分。但是 Borda 赢家并不一定是独立的,在一名其它选手退出之后,原来的 Borda 赢家有可能不再是 Borda 赢家。Condorcet 赢家不一定是 Borda 积分制的赢家,但是幸运的是,如果我们照样定义出 Condorcet 输家的概念,那么它一定不会是 Borda 积分制的赢家。因此这种判断法虽然并不和 Borda 规则重合,至少不会太差。这两个规则都至少需要四人之间两两之间对决一次,就是 6 次。我觉得我应该可以证明,6 次的情况下 Condorcet 赢家应该会和 Borda 赢家重合,但是我证明不了,摔!公平和效率是不可兼得的。我们可以重复20轮比赛来排除运气的因素,以达到更公平的结果,但是这是要付出代价的。同样,我们也可以选择 4 进 2 然后 2 进 1 的方式,这样就只需要进行四场比赛,但是这同样是依赖于分组抽签的运气的。虽然不知道你们更喜欢 Borda 计分法还是 Condorcet 赢家(+删除场数的拓展),但是我更喜欢 Borda。由于这两个规则都是匿名并且中立的,并且满足一致同意性原则,因此根据阿罗不可能性定理,一定会遇到违反独立无关性条件的情况。但是这个就是细节问题了。毕竟如果我们将投票看作是信息整合的过程,我们从海量的选票中最终整理出来一个排序,这无非就是以抛弃大量信息为代价的。
好了不想写了。
打循环赛,100轮。
不会一考定终身了,不能说意外了吧?
参考世界杯小组赛,采用积分制,最后出线的两只队争冠军。
配给制
这个问题是一个典型的数学建模问题,我来试着做一下吧!
一、模型简述
我们假设有n支队伍需要排名次,为了简化问题,我们让他们两两对决,然后在每次比赛只分出胜负而不计比分和每次比赛计比分两种情况,建立不同的模型来解决。其中前者引入竞赛图,通过双向联通竞赛图的性质解决;而后者则利用比分矩阵的性质解决。
二、模型假设:
1.不考虑“场次最少”,使之两两对决,进行n(n-1)/2场比赛;
2.模型1中比赛是没有平局的,模型2中可以让每场比赛的比分均不等。
三、模型建立及求解
3.1 模型1的建立及求解
在模型1的情况下,我们用图来表示比赛结果。令图的顶点表示球队,而用连接两个顶点的、以箭头标明方向的边表示比赛结果,由胜方指向负方。如图所示: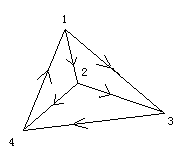

即1队战胜了2,3队,2队战胜了3,4队等等。
排名办法之一就是在图中顺着箭头找一条通过所有4个点的路径,如1->2->3->4,然而这种路径不止一条,如还可以找2->4->1->3,所以这种方法不能决定排名。
另一个方法是计算得分,即胜利次数。比如上图中四支队伍得分分别为2,2,1,1,;然而1,2两队,3,4两队之间就无法说明了。
为此我们用图论知识来解决这个问题。
竞赛图及其性质大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!
所有边均有向的图叫做有向图,每对顶点之间均有一条边的有向图称为竞赛图,问题归结为如何由竞赛图排名次。
2个顶点的竞赛图显然可以排出。
3个顶点的竞赛图有两种情况,如下图所示: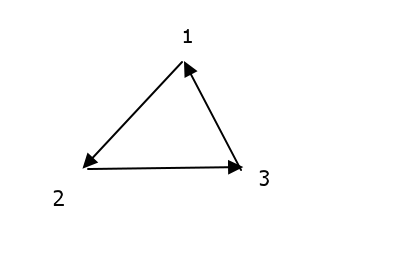

其中第一种情况是无法排序的,第二种情况显然是2->3->1.
而4个顶点的竞赛图共有4种形式,下面分别讨论。
(1)有唯一通过全部顶点的有向路径1->2->3->4,这种路径叫做完全路径,显然这就是排名顺序。
(2)这种情况2显然第一,其余3点满足上文中3个顶点竞赛图的第1种模式,所以排名为{2,(1,3,4)}
(3)同(2),显然名次为{(1,3,4),2}.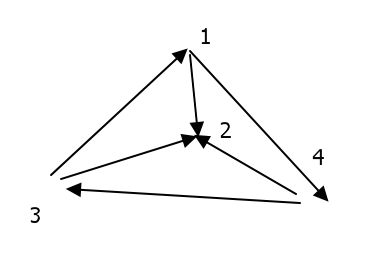

(4)如下图所示,有不止一条完全路径,无法简单地排序。
注意到(4)具有前三者没有的性质:对于任意一对顶点,存在两条有向路径,这种有向图称为双向连通的。
可以证明,所有竞赛图均可归为以下三类中的一类:
1.有唯一完全路径;
2.双向连通;
3.其他类型。
其中1的排名为唯一完全路径,3中必有对称情况,并列后可转化为1或2,所以重点研究2的情况。
双向连通竞赛图名次
定义竞赛图邻接矩阵 如下:
如下:
 如果从顶点i到j有一条有向边
如果从顶点i到j有一条有向边
0,else
则上图中双向连通图的邻接矩阵为
记顶点的得分向量为 ,其中
,其中 是第i个顶点的得分,则
是第i个顶点的得分,则 ,即A矩阵乘上一个n维的全1向量,易知上图得分向量为
,即A矩阵乘上一个n维的全1向量,易知上图得分向量为 ,依然无法排出名次,不过我们可以继续计算,令
,依然无法排出名次,不过我们可以继续计算,令 ,则
,则 ,可以证明,越往后算这个向量的排名就越合理,若
,可以证明,越往后算这个向量的排名就越合理,若 时这个向量收敛,那么我们就用其作为排名依据。
时这个向量收敛,那么我们就用其作为排名依据。
可以证明,这个极限是存在的,具体的证明后边再说,下面我们讨论每场比赛均有比分的情况。
3.2模型2的建立及求解
有n个运动员,同一项目同一标准下进行竞赛,i与j的得分之比为 ,如何排序?
,如何排序?
我们设每个运动员的评分向量归一化后的结果为 ,则
,则 ,比分矩阵
,比分矩阵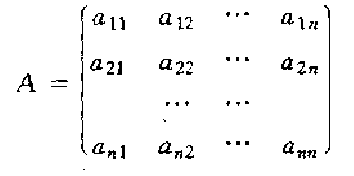
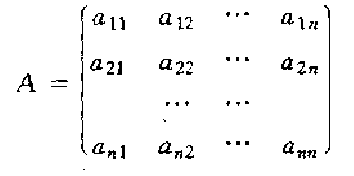
就变成了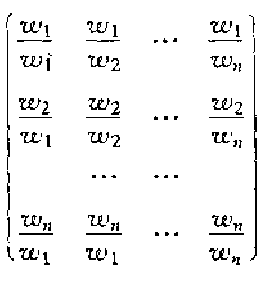

则有 ,
, 又称权向量。由于矩阵特征值之和等于主对角线元素之和,又主对角线元素之和为n,这说明n是A的最大特征值,称为主特征值,对应的特征向量称为主特征向量。
又称权向量。由于矩阵特征值之和等于主对角线元素之和,又主对角线元素之和为n,这说明n是A的最大特征值,称为主特征值,对应的特征向量称为主特征向量。
那么主特征向量是否一定存在呢?答案是肯定的。寻找的方法是迭代法,证明下文马上给出。
3.3极限得分向量存在性证明
对于n个顶点的双向连通竞赛图,存在正数r使得邻接矩阵A满足 ,这样的A称为素阵。
,这样的A称为素阵。
由Perron-Frobenius定理,素阵A的最大特征根为正单根 ,其对应的特征向量为s,且有
,其对应的特征向量为s,且有

所以模型1,2的最终结果都是其矩阵的最大特征值对应的特征向量,在实际中,往往采用迭代法来求此特征向量。
四、模型修正
在上述模型2中直接使用A矩阵是有道理的,但是仍然有不合理性:因为加权向量是各队水平之比,而结果却是各队的得分。因此更好的方法是让某个矩阵B的元素代表二者真实水平之比,那么问题来了,怎么计算B?
一个很自然的想法是上述得分的比值,即 ,但是这样仍然有一个问题,就是万一分母为0怎么办。我们可以假设每个队伍有一个基础的分数(知乎的排名算法对赞同数为0的答案无效,因此采取的办法是默认回答者对自己的答案有一票赞同)a,那么令
,但是这样仍然有一个问题,就是万一分母为0怎么办。我们可以假设每个队伍有一个基础的分数(知乎的排名算法对赞同数为0的答案无效,因此采取的办法是默认回答者对自己的答案有一票赞同)a,那么令
 大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!
大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!
再用B的特征向量计算排名会合理很多。
五、参考文献
[1]姜启源,谢金星,叶俊,数学模型。北京,高等教育出版社,2011年1月。
[2]王树禾,数学模型基础,合肥,中国科学技术大学出版社,1996年5月。
[3]陈理荣,数学建模导论,北京邮电大学出版社。
[4]Perron
,Perron定理,维基百科。







